Although the rotary disc viscometer can measure the viscosity of the fluid relatively quickly, its accuracy is relatively , because the data measured with it generally need to be corrected . For Newtonian fluids, this instrument is relatively accurate, but not for non-Newtonian fluids , because it cannot measure the shear stress of the fluid in a narrow range . Admittedly, it 's still a useful and lightweight instrument.
Theoretically, suppose there is a fluid cylinder of height x, which is bounded by two parallel disks, both of radius R, see Fig. 19-27. Let the upper disk rotate at a constant angular velocity ω rad/s under the action of a couple force M, while the lower disk is stationary. The fluid in contact with the rotating disk above also rotates at an angular velocity ω , and the fluid in contact also remains stationary. The disk-shaped fluid layer between the two disks rotates at a moderate angular velocity.
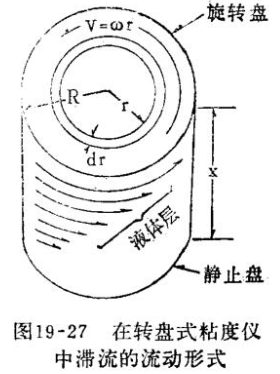
Assume another fluid drop shell with radius r and thickness dr rotates concentrically with the rotating upper disk. The velocity of the uppermost fluid in this shell isω r , the velocity of the fluid in the bottom layer is zero. Since the height of the shell is x, the velocity gradient (shear rate) through the shell height is:
γ = ω r/x
Let dM be the couple force acting on the ring of the shell (of area 2xr dr ). Then the force acting on the ring is dM/r, and the shear stress is:

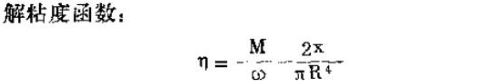
The viscosity measured by the above formula is the theoretical viscosity measured under satisfactory conditions (see Figure 19-27). There are actually a ton of side effects involved. And when the general portable rotary disc viscometer is measured, its rotating disc is immersed in a certain distance below the flow surface , so that it has two shear zones, one on the top of the disc and one on the bottom of the disc. under. The fluid cylinder above the disk is the surface of the measured fluid itself, which can be assumed to be a completely static fluid layer when the disk rotates, and the fluid cylinder below the disk is subject to a certain range of shear. This difference is easily seen in a hand-held disc viscometer, so it is necessary to calibrate the instrument with a fluid of known viscosity.
In order to compensate for the edge effect, the radius of the disc can be increased by assuming an increase of (2 In2/π)x, or 0.44x (x is the depth of the disc immersed in the fluid) for approximate compensation, so that it can be close to the actual situation some.






