Described below are some of the more important properties related to the ease of application of coatings in solution or suspension. Most wet coatings are applied by brush (like paint) or spray (like some epoxies used as insulators). Solution coatings are mainly based on polymers, and the rheological properties of polymer solutions are reviewed; in addition, some properties of suspensions are also discussed.
1. Polymer solution viscosity
While some theories of polymer solutions investigate the dependence of viscoelastic properties on molecular parameters, we do not discuss these here. Instead, we will focus on some generally accepted empirical relationships. Most are covered extensively by Ferry.
1) Dependence on molecular weight
For pure polymers, the dependence of molecular weight is usually expressed as a relationship of the following type:

In the formula, n0 is the "zero shear" viscosity, and K is a constant related to solvent and temperature. The value of the index ß is determined by the molecular weight range considered:
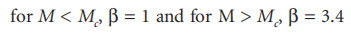
where M is the critical molecular weight that indicates the initiation of entanglement between molecules. The size of M is characteristic of the polymer structure; some representative figures are given in Table 4.1.
Although M marks the onset of topological effects on viscosity, it is not the same as the molecular weight M between entanglements (the latter amount is estimated from the magnitude of the rubber plateau modulus). about we have
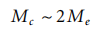
M is also a function of polymer concentration. In pure polymer (superscript 0) it reaches its lowest value M?; in solution at concentration C its size changes as described.
Only when the measured viscosity is at the so-called zero shear rate limit, the index takes the value in Equation 4.3. At higher rates, ß has lower values than unity and 3.4 in both cases.
2) Concentration dependence of viscosity
As mentioned above, below a certain concentration of C*, the entanglement effect is insignificant. This concentration is estimated from:
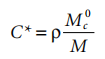
where M is the molecular weight of the polymer in the coating solution. However, the concentration C* cannot be estimated from a plot of η0 versus concentration; the transition is not sharp but gradual. 4 There is no single expression for concentration below C*
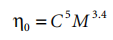
; However, in entangled states, this expression holds for some polymers. This relationship does not always hold for pure polymers, where higher indices are found. 6 Equation 4.5 also does not hold in the case of polymer solutions where there are other specific attractions such as poly(n-alkyl acrylate).
There are two reasons for the decrease in the viscosity of the polymer upon dilution: (a) the dilution effect, resulting in a solution viscosity intermediate between the two pure components, and (b) due to the lower Tg after dilution. The latter is solvent-specific and is the main reason why it is difficult to establish a general viscosity-concentration relationship for polymer solutions.
2. The viscosity of the suspension
Many latex paints are suspensions in water or organic solvents. Their rheological properties differ from polymer solutions in several respects. The form of concentration dependence differs and, moreover, depends on particle size. Also, at high concentrations, these suspensions tend to have structure, often referred to as aggregated networks. The direct consequences of the existence of pseudo-networks are yield stress and thixotropy phenomena. Next, we will explore the relationship between these quantities and the properties of the particles that make up the suspension.
1) The relationship between viscosity and concentration
In dilute suspensions, the concentration dependence is represented by an extension of Einstein's equation:
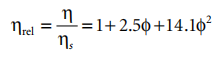
In the formula, n is the viscosity of the solvent, and φ is the volume fraction of the suspension. For spherical particles with no interparticle interactions, Equation 4.6 is valid. Including long-range interactions (such as volume exclusion) changes only φ2.
Of more interest are the rheological phenomena that occur in suspensions of particles with short-range interactions (attraction or repulsion). Through comprehensive research, Matsumoto et al. established the conditions for the existence of yield stress in suspension. Their conclusions are as follows:
1 - For particles with repulsive interactions, there is no yield stress.
2 -- A suspension of neutral particles, or attractive particles, does exhibit a yield stress.
3—The size of the yield stress increases with the increase of particle concentration and surface area to volume ratio.
In this study, the presence of yield stress was inferred by the presence of plateaus in the elastic modulus G', with low frequency; the magnitude of the yield stress was deduced from the height of the plateau modulus.






