Developments in the field of microelectronics have enabled the fabrication of micro-media sensors that can analyze drying, curing and diffusion phenomena in coatings. Over the past few years, several microdielectric sensors have been developed, the most sensitive being based on interdigitated electrodes and field effect transistors fabricated on 3 × 5 mm silicon wafers. Chip sensors are packaged in polyamide packages and configured for easy placement in a variety of processing environments.
The dielectric response results from moving dipoles and ions in the material being measured. When the coating cured, the mobility of dipoles and ions was greatly reduced, sometimes by as much as seven orders of magnitude. Microdielectric sensors are sensitive enough to track these changes and are therefore useful for cure monitoring, cure analysis, and process control. Dielectric response is typically expressed in terms of dielectric constant or dielectric constant (E') and dissipation factor (E"):

where (E, - E)/(1 + wt) is the dipole term, segw is the conductivity term,
E' = dielectric constant
E" = loss factor
S = bulk ionic conductivity
E0 = permittivity of free space (a constant)
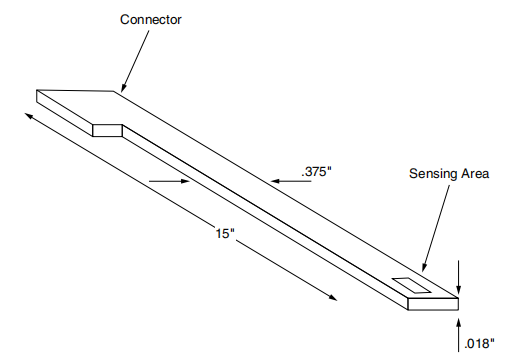
Figure 13.1 Schematic diagram of micro-media sensor
ω = frequency x 2π
τ = dipole relaxation time
Er = Relaxed permittivity (low frequency E′ )
Eu = Unrelaxed permittivity (high frequency E′)
In addition to ions and dipoles, factors such as electrode polarization or inhomogeneity also affect the dielectric response; however, these usually play a minor role and are generally ignored.
Dielectric dissipation factor is a useful quantity to monitor the curing reaction. Dipole relaxation times or ionic conductivity levels can be monitored during curing. However, dipole relaxation times are often difficult to determine because the conductivity response usually dominates the dipole term in Equation 13.2. Conductivity, on the other hand, can usually be determined throughout the curing process, especially by monitoring low frequencies (< 10 Hz) at the end of the cure. The inverse of the measured conductivity, or resistivity, is often directly proportional to the viscosity of the material being tested before gelling, and related to the stiffness after gelling.
