There are generally four methods used for contact angle measurements in stationary droplets.
1. Half-angle fitting/height-width method
2. Circle fitting method
3. Ellipse fitting method
4. Tangent fitting method
Half-width fit/height-width method
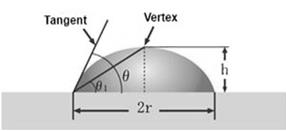
If the droplet size is small, its shape can be assumed to be part of a sphere, and the 2D profile of the droplet is circular.
Here h is the height and r is half the width of the baseline. So θ1 =tan -1h/r. And the contact angle θ = 2θ 1 can be proved by simple geometry (see adjacent figure). By calculating h and r by image analysis, the contact angle θ can be measured.
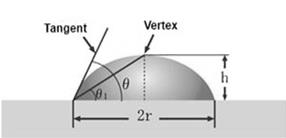
This approach works well for smaller sized droplets with symmetrical shapes. For larger sized droplets, gravity may reduce the apex height.
circular fit
The process of calculating the contact angle by the circle fitting method is as follows:
Capture drag and drop images and save them.
Check the baseline.
Select 3 or more points on the edge of the curved droplet outline.
Fit a circular curve with this selected point and find the equation of the circle.
Find the tangential angle between the two points where the circle intersects the baseline and the baseline. This actually represents the contact angle.
The circle fitting method is a widely used method for calculating contact angle due to its high accuracy. Especially suitable for the calculation of contact angles less than 30°. This approach has limitations for larger sized droplets and asymmetric droplets.
Ellipse fitting
In the ellipse fitting method, elliptic curve fitting of the droplet profile is used. The process is similar to circle fitting.
Capture drag and drop images and save them.
Check the baseline.
Here the curve edge requires at least 6 guess points for curve fitting.
Find the equation of the fitted ellipse.
Find the tangent angle to the baseline at the two intersection points of this ellipse with the baseline. This actually represents the contact angle.
The difference is that the algorithm of ellipse fitting is very complicated. Can be used to calculate contact angles based on static drops over a wide range (0-130°)
Tangent fit
The shape of the droplet is assumed to be part of the outline of an imaginary circle. This method obtains the center of an imaginary circle and determines the contact angle as an angle and a line tangent to the circle.
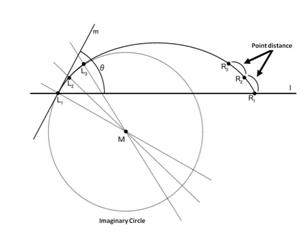
An imaginary circle is formed from the three arc points L1, L2 and L3 in the figure below. The angle between the tangent m and the descending baseline l is the left contact angle. The correct contact angle can be measured in the same way using points R1, R2 and R3.




